F Statistics¶
F3 Statistics¶
F3 statistics are a useful analytical tool to understand population relationships. F3 statistics, just as F4 and F2 statistics measure allele frequency correlations between populations and were introduced by Nick Patterson in his Patterson 2012
F3 statistics are used for two purposes: i) as a test whether a target population (C) is admixed between two source populations (A and B), and ii) to measure shared drift between two test populations (A and B) from an outgroup (C).
F3 statistics are in both cases defined as the product of allele frequency differences between population C to A and B, respectively:
Here, \(\langle\cdot\rangle\) denotes the average over all genotyped sites, and \(a, b\) and \(c\) denote the allele frequency for a given site in the three populations \(A, B\) and \(C\).
Admixture F3 Statistics¶
It can be shown that if that statistics is negative, it provides unambiguous proof that population C is admixed between populations A and B, as in the following phylogeny (taken from Figure 1 from Patterson 2012):
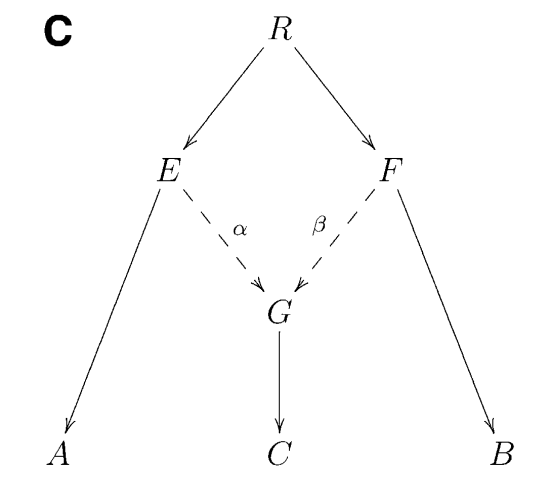
Intuitively, an F3 statistics becomes negative if the allele frequency of the target population (C) is on average intermediate between the allele frequencies of A and B. Consider as an extreme example a genomic site where \(a=0, b=1\) and \(c=0.5\). Then we have \((c-a)(c-b)=-0.25\), which is negative. So if the entire statistics is negative, it suggests that in many positions, the allele frequency \(c\) is indeed intermediate, suggesting admixture between the two sources.
Note
If an F3 statistics is not negative, it does not proof that there is no admixture!
We will use this statistics to test if Finnish are admixed between East and West, using different Eastern and Western sources. In the West, we use French, Icelandic, Lithuanian and Norwegian as source, and in the East we use Nganasan and one of the populations analysed in this workshop, Bolshoy Oleni Ostrov, a 3,500 year old group from the Northern Russian Kola-peninsula.
We use the software qp3Pop from AdmixTools, which similar to smartpca takes a parameter file:
genotypename: input genotype file (in eigenstrat format)
snpname: input snp file (in eigenstrat format)
indivname: input indiv file (in eigenstrat format)
popfilename: a file containing rows with three populations on each line A, B and C.
inbreed: YES
Here, the last option is necessary if we are analysing pseudo-diploid ancient data (which is the case here).
To prepare the popfilename, open a new file using Jupyter and enter:
Nganasan French Finnish
Nganasan Icelandic Finnish
Nganasan Lithuanian Finnish
Nganasan Norwegian Finnish
BolshoyOleniOstrov French Finnish
BolshoyOleniOstrov Icelandic Finnish
BolshoyOleniOstrov Lithuanian Finnish
BolshoyOleniOstrov Norwegian Finnish
Exercise
Prepare the parameter file with the input data as in the PCA session (see Principal Components Analysis (PCA)) and then run qp3Pop -p PARAMETER_FILE, where PARAMETERFILE should be replaced by your parameter file name. This will take about 3 minutes (see the ~/share/solutions/bash_commands notebook if you need a hint).
The results are in the output that you can view in the Notebook. The crucial bit should look like this:
Source 1 Source 2 Target f_3 std. err Z SNPs
result: Nganasan French Finnish -0.004539 0.000510 -8.894 442567
result: Nganasan Icelandic Finnish -0.005297 0.000563 -9.404 427954
result: Nganasan Lithuanian Finnish -0.005062 0.000590 -8.574 426231
result: Nganasan Norwegian Finnish -0.004744 0.000569 -8.332 428161
result: BolshoyOleniOstrov French Finnish -0.002814 0.000444 -6.341 402958
result: BolshoyOleniOstrov Icelandic Finnish -0.002590 0.000486 -5.323 386418
result: BolshoyOleniOstrov Lithuanian Finnish -0.001523 0.000536 -2.840 384134
result: BolshoyOleniOstrov Norwegian Finnish -0.001553 0.000502 -3.092 386203
This output shows as first three columns the three populations A, B (sources) and C (target). Then the f3 statistics, which is negative in all cases tested here, a standard error, a Z score and the number of SNPs involved in the statistics.
The Z score is key: It gives the deviation of the f3 statistic from zero in units of the standard error. As general rule, a Z score of -3 or more suggests a significant rejection of the Null hypothesis that the statistic is not negative. In this case, all of the statistics are significantly negative, proving that Finnish have ancestral admixture of East and West Eurasian ancestry. Note that the statistics does not suggest when this admixture happened!
F4 Statistics¶
A different way to test for admixture is by “F4 statistics” (or “D statistics” which is very similar), also introduced in Patterson 2012.
F4 statistics are also defined in terms of correlations of allele frequency differences, similarly to F3 statistics (see above), but involving four different populations, not just three. Specifically we define
To understand the statistics, consider the following tree:
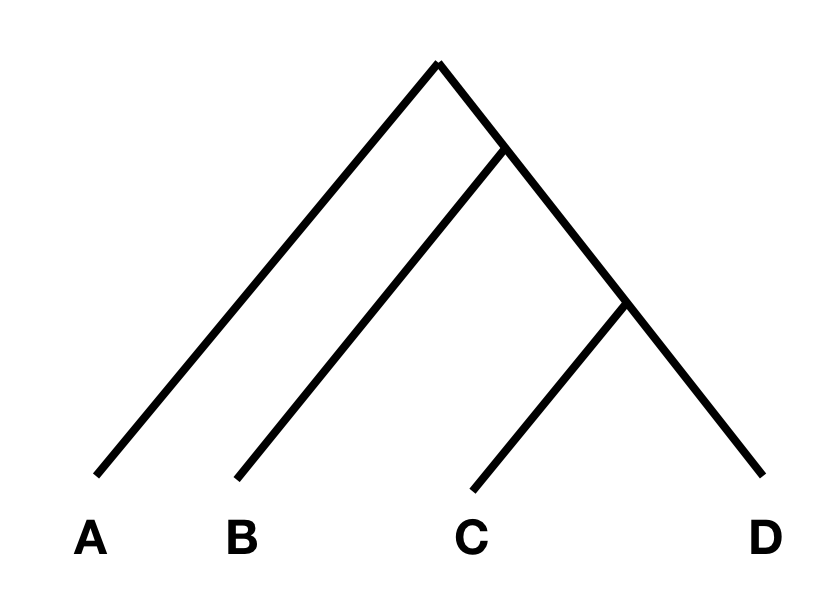
In this tree, without any additional admixture, the allele frequency difference between A and B should be completely independent from the allele frequency difference between C and D. In that case, F4(A, B; C, D) should be zero, or at least not statistically different from zero. However, if there was gene flow from C or D into A or B, the statistic should be different from zero. Specifically, if the statistic is significantly negative, it implies gene flow between either C and B, or D and A. If it is significantly positive, it implies gene flow between A and C, or B and D.
The way this statistic is often used, is to put a divergent outgroup as population A, for which we know for sure that there was no admixture into either C or D. With this setup, we can then test for gene flow between B and D (if the statistic is positive), or B and C (if it is negative).
Here, we can use this statistic to test for East Asian admixture in Finns, similarly to the test using Admixture F3 statistics above. We will use the qpDstat program from AdmixTools for that. We need to again prepare a population list file, this time with four populations (A, B, C, D). I suggest you open a new file and fill it with:
Mbuti Nganasan French Finnish
Mbuti Nganasan Icelandic Finnish
Mbuti Nganasan Lithuanian Finnish
Mbuti Nganasan Norwegian Finnish
Mbuti BolshoyOleniOstrov French Finnish
Mbuti BolshoyOleniOstrov Icelandic Finnish
Mbuti BolshoyOleniOstrov Lithuanian Finnish
Mbuti BolshoyOleniOstrov Norwegian Finnish
You can then use this file again in a parameter file, similar to the one prepared for qp3Pop above:
genotypename: input genotype file (in eigenstrat format)
snpname: input snp file (in eigenstrat format)
indivname: input indiv file (in eigenstrat format)
popfilename: a file containing rows with three populations on each line A, B and C.
f4mode: YES
Note that you cannot give the “inbreed” option here.
Exercise
Prepare the parameter file as suggested above and then run qpDstat -p PARAMETER_FILE, where PARAMETERFILE should be replaced by your parameter file name. This will take about 3 minutes (see the ~/share/solutions/bash_commands notebook if you need a hint).
The results should be (skipping some header lines):
result: Mbuti Nganasan French Finnish 0.002363 19.016 29254 27852 593124
result: Mbuti Nganasan Icelandic Finnish 0.001721 11.926 28915 27894 593124
result: Mbuti Nganasan Lithuanian Finnish 0.001368 9.664 28745 27933 593124
result: Mbuti Nganasan Norwegian Finnish 0.001685 11.663 28933 27934 593124
result: Mbuti BolshoyOleniOstrov French Finnish 0.001962 16.737 27249 26175 547486
result: Mbuti BolshoyOleniOstrov Icelandic Finnish 0.001084 7.776 26876 26282 547486
result: Mbuti BolshoyOleniOstrov Lithuanian Finnish 0.000554 3.942 26683 26380 547486
result: Mbuti BolshoyOleniOstrov Norwegian Finnish 0.000952 6.707 26873 26351 547486
Here, the key columns are columns 2, 3, 4 and 5, denoting A, B, C and D, and column 6 and 7, which denote the F4 statistic and the Z score, measuring significance in difference from zero.
As you can see, in all cases, the Z score is positive and larger than 3, indicating a significant deviation from zero, and implying gene flow between Nganasan and Finnish, and BolshoyOleniOstrov and Finnish, when compared to French, Icelandic, Lithuanian or Norwegian.
Outgroup F3 Statistics¶
Outgroup F3 statistics are a special case how to use F3 statistics. The definition is the same as for Admixture F3 statistics, but instead of a target C and two source populations A and B, one now gives an outgroup C and two test populations A and B.
To get an intuition for this statistics, consider the following tree:
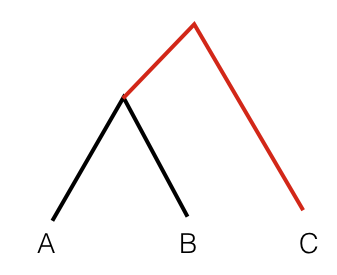
In this scenario, the statistic F3(A, B; C) measures the branch length from C to the common ancestor of A and B, coloured red. So this statistic is simply a measure of how closely two population A and B are related with each other, as measured from a distant outgroup. It is thus a similarity measure: The higher the statistic, the more genetically similar A and B are to one another.
We can use this statistic to measure for example the the genetic affinity to East Asia, by performing the statistic F3(Han, X; Mbuti), where Mbuti is a distant African population and acts as outgroup here, Han denote Han Chinese, and X denotes various European populations that we want to test.
You need to start, again, by preparing a list of population triples to be measured. I suggest the following list:
Han Chuvash Mbuti
Han Albanian Mbuti
Han Armenian Mbuti
Han Bulgarian Mbuti
Han Czech Mbuti
Han Druze Mbuti
Han English Mbuti
Han Estonian Mbuti
Han Finnish Mbuti
Han French Mbuti
Han Georgian Mbuti
Han Greek Mbuti
Han Hungarian Mbuti
Han Icelandic Mbuti
Han Italian_North Mbuti
Han Italian_South Mbuti
Han Lithuanian Mbuti
Han Maltese Mbuti
Han Mordovian Mbuti
Han Norwegian Mbuti
Han Orcadian Mbuti
Han Russian Mbuti
Han Sardinian Mbuti
Han Scottish Mbuti
Han Sicilian Mbuti
Han Spanish_North Mbuti
Han Spanish Mbuti
Han Ukrainian Mbuti
Han Levanluhta Mbuti
Han BolshoyOleniOstrov Mbuti
Han ChalmnyVarre Mbuti
Han Saami.DG Mbuti
which cycles through many populations from Europe, including the ancient individuals from Chalmny Varre, Bolshoy Oleni Ostrov and Levänluhta.
Exercise
Copy this list into a file, and prepare a parameter file for running qp3Pop, similar to the parameter file for admixture F3 statistics above, and run qp3Pop with that parameter file as above.
You should find this (skipping header lines from the output):
Source 1 Source 2 Target f_3 std. err Z SNPs
result: Han Chuvash Mbuti 0.233652 0.002072 112.782 502678
result: Han Albanian Mbuti 0.215629 0.002029 106.291 501734
result: Han Armenian Mbuti 0.213724 0.001963 108.882 504370
result: Han Bulgarian Mbuti 0.216193 0.001979 109.266 504310
result: Han Czech Mbuti 0.218060 0.002002 108.939 504089
result: Han Druze Mbuti 0.209551 0.001919 109.205 510853
result: Han English Mbuti 0.216959 0.001973 109.954 504161
result: Han Estonian Mbuti 0.220730 0.002019 109.332 503503
result: Han Finnish Mbuti 0.223447 0.002044 109.345 502217
result: Han French Mbuti 0.216623 0.001969 110.012 509613
result: Han Georgian Mbuti 0.214295 0.001935 110.721 503598
result: Han Greek Mbuti 0.215203 0.001984 108.465 507475
result: Han Hungarian Mbuti 0.217894 0.001999 109.004 507409
result: Han Icelandic Mbuti 0.218683 0.002015 108.553 504655
result: Han Italian_North Mbuti 0.215332 0.001978 108.854 507589
result: Han Italian_South Mbuti 0.211787 0.002271 93.265 492400
result: Han Lithuanian Mbuti 0.219615 0.002032 108.098 503681
result: Han Maltese Mbuti 0.210359 0.001956 107.542 503985
result: Han Mordovian Mbuti 0.223469 0.002008 111.296 503441
result: Han Norwegian Mbuti 0.218873 0.002023 108.197 504621
result: Han Orcadian Mbuti 0.217773 0.002014 108.115 504993
result: Han Russian Mbuti 0.223993 0.001995 112.274 506525
result: Han Sardinian Mbuti 0.213230 0.001980 107.711 508413
result: Han Scottish Mbuti 0.218489 0.002039 107.145 499784
result: Han Sicilian Mbuti 0.212272 0.001975 107.486 505477
result: Han Spanish_North Mbuti 0.215885 0.002029 106.383 500853
result: Han Spanish Mbuti 0.213869 0.001975 108.297 513648
result: Han Ukrainian Mbuti 0.218716 0.002007 108.950 503981
result: Han Levanluhta Mbuti 0.236252 0.002383 99.123 263049
result: Han BolshoyOleniOstrov Mbuti 0.247814 0.002177 113.849 457102
result: Han ChalmnyVarre Mbuti 0.233499 0.002304 101.345 366220
result: Han Saami.DG Mbuti 0.236198 0.002274 103.852 489038
Now it’s time to plot these results using python.
Exercise
Copy the results (all lines from the output beginning with “results:”) into a text file, open a Jupyter python3 notebook and load the text file into a pandas dataframe, using pd.read_csv(FILENAME, delim_whitespace=True, names=["dummy", "A", "B", "C", "F3", "StdErr", "Z", "SNPS"]. View the resulting dataframe and make sure it looks correct.
A useful way to plot these results is by sorting them by the F3 statistics, and then plotting the test populations from left to right, beginning with the largest values. This code snippet should do the trick:
d=f3dat_han.sort_values(by="F3")
y = range(len(d))
plt.figure(figsize=(6, 8))
plt.errorbar(d["F3"], y, xerr=d["stderr"], fmt='o')
plt.yticks(y, d["B"]);
plt.xlabel("F3(Han, Test; Mbuti)");
Exercise
Use the above code snippet to plot the Outgroup F3 data. Google the errorbar and yticks functions from matplotlib if you want to know how they works.
You should get something like this:
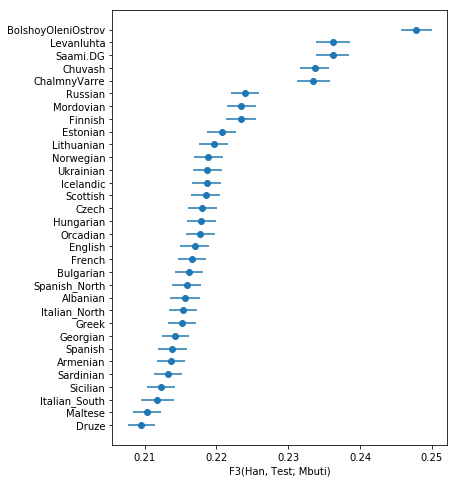
showing that, as expected, The ancient samples and modern Saami are most closely related to modern East Asians (as represented by Han) compared to many other Europeans.
Outgroup F3 Statistics Biplot¶
The above plot shows an intriguing cline of differential relatedness to Han in many Europeans. For example, would you have guessed that Icelandics are closer to Han than Armenians are to Han? This is very surprising, and it shows that European ancestry has a complex relationship to East Asians. To understand this better, you can read Patterson 2012, who makes some intriguing observations. Patterson and colleagues use Admixture F3 statistics and apply it to many populations world-wide. They summarise some population triples with the most negative F3 statistics in the following table:

There are many interesting results here, but one of the most striking one is the finding of F3(Sardinian, Karitiana; French), which is highly significantly negative. This statistics implies that French are admixed between Sardinians and Karitiana, a Native American population from Brazil. How is that possible? We can of course rule out any recent Native American backflow into Europe.
Patterson and colleagues explained this finding with hypothesising an ancient admixture event, from a Siberian population that contributed to both Europeans and to Native Americans. They termed that population the “Ancient North Eurasians (ANE)”. The following admixture graph was suggested:
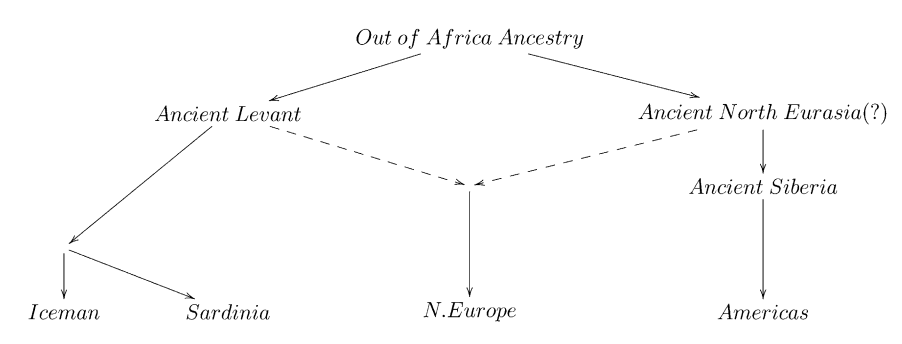
As you can see, the idea is that modern Central Europeans, such as French, are admixed between Southern Europeans (Sardinians) and ANE. The Ancient North Eurasians are a classic example for a “Ghost” population, a population which does not exist anymore in unmixed form, and from which we have no direct individual representative.
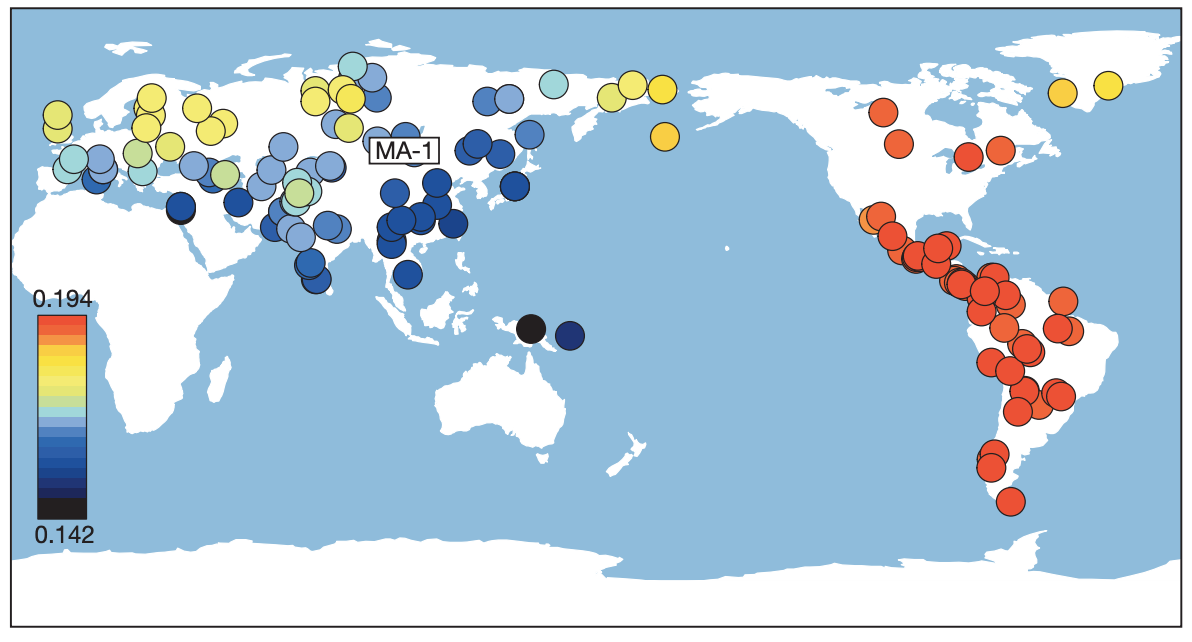
Amazingly, two years after the publication of Patterson 2012, the ANE ghost population was actually found: Raghavan et al. and colleagues, in 2014, published a paper called “Upper Palaeolithic Siberian genome reveals dual ancestry of Native Americans”. A 24,000 year old boy (called MA1) from the site of “Mal’ta” in Siberia was shown to have close genetic affinity with both Europeans and in particular Native Americans, just as proposed in Patterson 2012.
The affinities are summarised nicely in this figure from Raghavan et al.:
OK, so we now know that ancestry related to Native Americans contributed to European countries. Could that possibly explain the affinity of our ancient samples and Saami to Han Chinese in some way? To test this, we will run the same Outgroup F3 statistics as above, but this time not with Han but with MA1 as test population. Specifically, we run the following population triples in qp3Pop:
MA1_HG.SG Chuvash Mbuti
MA1_HG.SG Albanian Mbuti
MA1_HG.SG Armenian Mbuti
MA1_HG.SG Bulgarian Mbuti
MA1_HG.SG Czech Mbuti
MA1_HG.SG Druze Mbuti
MA1_HG.SG English Mbuti
MA1_HG.SG Estonian Mbuti
MA1_HG.SG Finnish Mbuti
MA1_HG.SG French Mbuti
MA1_HG.SG Georgian Mbuti
MA1_HG.SG Greek Mbuti
MA1_HG.SG Hungarian Mbuti
MA1_HG.SG Icelandic Mbuti
MA1_HG.SG Italian_North Mbuti
MA1_HG.SG Italian_South Mbuti
MA1_HG.SG Lithuanian Mbuti
MA1_HG.SG Maltese Mbuti
MA1_HG.SG Mordovian Mbuti
MA1_HG.SG Norwegian Mbuti
MA1_HG.SG Orcadian Mbuti
MA1_HG.SG Russian Mbuti
MA1_HG.SG Sardinian Mbuti
MA1_HG.SG Scottish Mbuti
MA1_HG.SG Sicilian Mbuti
MA1_HG.SG Spanish_North Mbuti
MA1_HG.SG Spanish Mbuti
MA1_HG.SG Ukrainian Mbuti
MA1_HG.SG Levanluhta Mbuti
MA1_HG.SG BolshoyOleniOstrov Mbuti
MA1_HG.SG ChalmnyVarre Mbuti
MA1_HG.SG Saami.DG Mbuti
where MA1_HG.SG is the cryptic name for the MA1 genome from Raghavan et al..
Exercise
Follow the same protocol as above: Copy the list into a file, prepare a parameter file for qp3Pop with that population triple list, and run qp3Pop. Copy the results (all lines beginning with “results:”) into a file and load it into python via pd.read_csv().
To test in what way the relationship to Han Chinese is correlated with the relationship with MA1, we will now plot the two statistics against each other in a scatter plot. We first have to merge the two outgroup-F3 datasets together. Here is the code including loading (assuming that the two F3 dataframes are called outgroupf3dat_Han and outgroupf3dat_MA1):
outgroupf3dat_Han = pd.read_csv("/home/training/work/outgroupF3_results_Han.txt",
delim_whitespace=True,
names=["dummy", "A", "B", "C", "F3", "stderr", "Z", "nSNPs"])
outgroupf3dat_MA1 = pd.read_csv("/home/training/work/outgroupF3_results_MA1.txt",
delim_whitespace=True,
names=["dummy", "A", "B", "C", "F3", "stderr", "Z", "nSNPs"])
outgroupf3dat_merged = outgroupf3dat_Han.merge(outgroupf3dat_MA1, on="B", suffixes=("_Han", "_MA1"))
Exercise
run the above merge command and check that it worked by viewing the resulting dataframe.
Finally, we can produce our bi-plot, using this code:
plt.figure(figsize=(10, 10))
plt.scatter(x=outgroupf3dat_merged["F3_Han"], y=outgroupf3dat_merged["F3_MA1"])
plt.xlabel("F3(Test, Han; Mbuti)");
plt.ylabel("F3(Test, MA1; Mbuti)");
This should yield something like this:
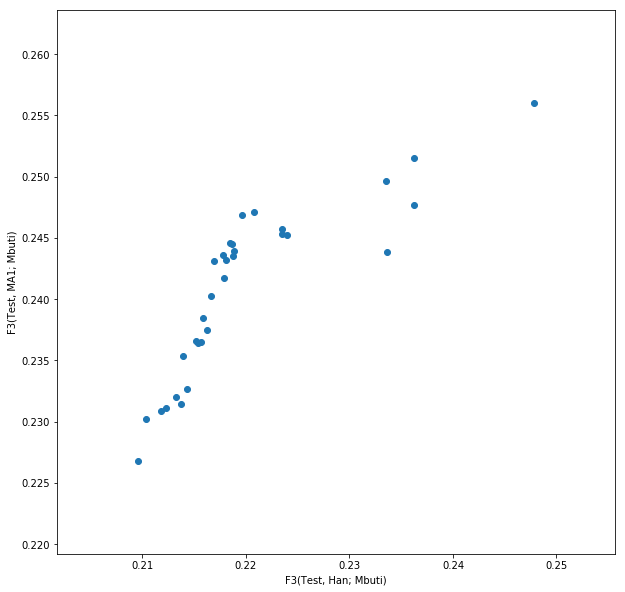
This isn’t very useful, however, as we cannot see which point is which population. We can use the annotation function from matplotlib to add text labels to each point:
plt.figure(figsize=(10, 10))
plt.scatter(x=outgroupf3dat_merged["F3_Han"], y=outgroupf3dat_merged["F3_MA1"])
for i, row in outgroupf3dat_merged.iterrows():
plt.annotate(row["B"], (row["F3_Han"], row["F3_MA1"]))
plt.xlabel("F3(Test, Han; Mbuti)");
plt.ylabel("F3(Test, MA1; Mbuti)");
which should yield:

Exercise
Create this plot with the code snippets above.
The result shows that indeed the affinity to East Asians in the bulk of European contries can be explained by MA1-related ancestry. Most European countries have a linear relationship between their affinity to Han and their affinity to MA1. However, this is not true for our ancient samples from Fennoscandia and for modern Saami and Chuvash, who have extra affinity to Han not explained by MA1 (Lazaridis et al. 2014).